2023-01-16

JavaScriptでコイントスをするプログラミング

こんにちは。今回は、Webページ上でコイントスをするプログラムをHTML/JavaScriptで作成しましたので共有します。

実装イメージ

「Flip Coin」ボタンを押すとコイントスが始まり、表か裏が表示されます。

HTML/JavaScriptコード

<button onclick="flipCoin()" style="font-size:100%">Flip Coin</button>
<div id="result"></div>
<img id="coin" style="display:none;">

<script>
function flipCoin() {
  var result = Math.floor(Math.random() * 2) + 1;
  var interval = setInterval(function() {
    if (result === 1) {
      document.getElementById("coin").src = "https://cdn-ak.f.st-hatena.com/images/fotolife/d/dskevin/20230108/20230108190854.jpg";  //表用の画像ファイルパス
      document.getElementById("coin").style.display = "block";
    } else {
      document.getElementById("coin").src = "https://cdn-ak.f.st-hatena.com/images/fotolife/d/dskevin/20230108/20230108190858.jpg"; //裏用の画像ファイルパス

      document.getElementById("coin").style.display = "block";
    }
    result = (result === 1) ? 2 : 1;
  }, 100);
  setTimeout(function() {
    clearInterval(interval);
  }, 1000);
}
</script>

ご参考

実はこちらのプログラムは、ChatGPT（https://openai.com/blog/chatgpt/）というAIを使って実装しています。

様子を動画にまとめていますので、よければこちらもご覧ください。
youtu.be

最後まで読んでいただきありがとうございました。

2022-10-09

スクリーンセーバー的なアニメーション動画の作成｜Processing

Processing

Processingについての投稿３回目です。今回は、ずっと見ていられるスクリーンセーバーのようなものを作りたいと思い、２つ実装してみました。どちらも、ぼーっと見ていられるアニメーションになっていると思います。

アニメーション

1つ目は、複数のボールが動きながら色を塗りつぶしていく動画です。ボールが跳ね返る度に、少しずつボールの色が変化していきます。スマートフォン向けに縦動画です。
youtube.com

2つ目は、ボール同士が衝突しながら合体し、大きくなっていく動画です。全てのボールが合体するとまたバラバラになります。PC向けに横動画です。
youtu.be

アニメーションのコード

カラフルなボールが平面を塗りつぶしていく動画

// 変数宣言
int ballnum = 60;  // 玉の数（初期値）
Point[] points = new Point[ballnum];

void setup() {
  size(540, 980);
  
  background(255);
  // カラーモード指定
  colorMode( HSB, 360, 100, 100, 100 );
  
  // 初期化
  for (int i=0; i<points.length; i++) {
    points[i] = new Point(random(width), random(height), random(-5, 5), random(-5, 5), random(20,100), random(0, 360), random(50, 60), random(90, 100));
    // x方向,y方向の移動速度を制御する変数は、√(x^2+y^2)で標準化した上で、サイズに応じた値を掛け算する
    points[i].speedX = 4 * 30/points[i].ballsize * points[i].speedX / sqrt(sq(points[i].speedX)+sq(points[i].speedY));
    points[i].speedY = 4 * 30/points[i].ballsize * points[i].speedY / sqrt(sq(points[i].speedX)+sq(points[i].speedY));
  }
}

void draw() {
  
  frameRate(60);
  //background(0);

  // 移動と描画
  for (int i=0; i<points.length; i++) {
    points[i].move();
    points[i].drawEllipse();
  }
   
  // 動画作成用にpngファイルを保存　※保存時にコメントインする
  //saveFrame("frames/######.png");

}

class Point {
  // 変数を宣言
  float x;  //
  float y;
  float speedX;
  float speedY;
  float ballsize;
  float col1; 
  float col2;
  float col3;

  // constractorを初期化
  Point(float _x, float _y, float _speedX, float _speedY, float _ballsize,
        float _col1, float _col2, float _col3) {
    x = _x;
    y = _y;
    speedX = _speedX;
    speedY = _speedY;
    ballsize = _ballsize;
    col1 = _col1;
    col2 = _col2;
    col3 = _col3;
  }

  // method 関数
  void move() {
    // x,y方向にそれぞれ移動
    x += speedX;
    y += speedY;
    
    // 玉が左端に到達したらx軸方向を逆向きにする
    // ※半径の幅を考慮してballsize/2としている
    if (x < ballsize/2){
      x = ballsize/2;
      speedX = -speedX;
      col1 += 10;
    }
    // 玉が右端に到達したらx軸方向を逆向きにする
    else if (x > width-ballsize/2) {
      x = width-ballsize/2;
      speedX = -speedX;
      col1 += 10;
    }
    // 玉が上端に到達したらy軸方向を逆向きにする
    if (y < ballsize/2){
      y = ballsize/2;
      speedY = -speedY;
      col1 += 10;
    }
    // 玉が下端に到達したらy軸方向を逆向きにする
    else if (y > height-ballsize/2){
      y = height-ballsize/2;
      speedY = -speedY;
      col1 += 10;
    }
    
    // 色相が360を超えたら360引く 
    if (col1 > 360){
      col1 -= 360;
    }
  }
  
  // 描画 
  void drawEllipse() {
    // 縁なし
    noStroke();
    
    // 玉の色を指定
    fill(col1, col2, col3, 50);
    
    // 位置とサイズを指定して、玉を表示
    ellipse(x, y, ballsize, ballsize);
  }
}

玉が衝突しながら大きくなっていく動画

// 変数宣言
int ballnum = 100;  // 玉の数（初期値）
int default_ballsize = 40;  // 玉のサイズ（初期値）
int base_speed=12; // 速度の基準値
int counter = 0; // リセット処理用カウンタ
boolean reset_flag = false;  // リセットフラグ
Point[] points = new Point[ballnum];

void setup() {
  
  // フルスクリーン表示
  fullScreen();

  // カラーモード指定
  colorMode( HSB, 360, 100, 100, 100 );
  
  // 初期化
  for (int i=0; i<points.length; i++) {
    points[i] = new Point(random(width), random(height), random(-5, 5), random(-5, 5), default_ballsize, random(0, 360), random(90, 100), random(90, 100));
    
    // x方向,y方向の移動速度を制御する変数は、2次元上での移動速度が全ての玉で一緒になるように、base_speed/√(x^2+y^2)で標準化する
    points[i].speedX = base_speed*points[i].speedX/sqrt(sq(points[i].speedX)+sq(points[i].speedY));
    points[i].speedY = base_speed*points[i].speedY/sqrt(sq(points[i].speedX)+sq(points[i].speedY));
  }
}

void draw() {
  
  //frameRate(20);
  background(0,0,0);

  // 移動と描画
  for (int i=0; i<points.length; i++) {
    points[i].move();
    points[i].drawEllipse();
  }
  
  // 玉同士の接触判定
  for (int i=0; i<points.length; i++) {
    for (int j=i+1; j<points.length; j++) {
      // どちらかの玉が既に接触済で、サイズ0になっていればスキップ
      if ((points[i].ballsize == 0) || (points[j].ballsize == 0)) {continue;}
      
      // 接触範囲 = 2つの玉の半径を足し算
      float range = points[i].ballsize/2 + points[j].ballsize/2;
      
      // 玉の中心同士の距離 = √((x1-x2)^2+(y1-y2)^2)
      float dist = sqrt(sq(points[i].x - points[j].x) + sq(points[i].y - points[j].y));
      
      // 距離が半径の和よりも近い場合は接触
      if (dist <= range) {
        
        // 2玉のうち、サイズが大きい方が残る
        if (points[i].ballsize >= points[j].ballsize){
          
          // 新しい玉の面積が、2つの玉の面積の足し算になるように調整
          points[i].ballsize = sqrt(sq(points[i].ballsize)+sq(points[j].ballsize));
          
          // 玉の大きさに応じて移動速度を設定
          points[i].speedX = base_speed*points[i].speedX / sqrt(sq(points[i].speedX)+sq(points[i].speedY)) * sqrt(default_ballsize / points[i].ballsize);
          points[i].speedY = base_speed*points[i].speedY / sqrt(sq(points[i].speedX)+sq(points[i].speedY)) * sqrt(default_ballsize / points[i].ballsize);
          
          // 小さい方の玉のサイズを0にして表示から消す
          points[j].ballsize = 0;
        }
        else {
          //jの方がサイズが大きい場合の処理。内容は上と同じ
          points[j].ballsize = sqrt(sq(points[i].ballsize)+sq(points[j].ballsize));
          points[j].speedX = base_speed*points[j].speedX / sqrt(sq(points[j].speedX)+sq(points[j].speedY)) * sqrt(default_ballsize / points[j].ballsize);
          points[j].speedY = base_speed*points[j].speedY / sqrt(sq(points[j].speedX)+sq(points[j].speedY)) * sqrt(default_ballsize / points[j].ballsize);
          points[i].ballsize = 0;          
        }
      }
    }
  }
  
  // リセット判定
  int del_count = 0;
  // サイズが0になっている玉の数を確認
  for (int i=0; i<points.length; i++) {
    if (points[i].ballsize == 0){
      del_count += 1;
    }
  }
  // 全数-1がサイズ0になっていたらreset_flagをtrueにする
  if (del_count >= ballnum-1){
    reset_flag = true;
  }  
  
  // リセット処理
  if (reset_flag){
    // 回数カウンタを1追加
    counter += 1;
    
    // ボールの位置などを全て初期化
    for (int i=0; i<ballnum; i++) {
      points[i].x = random(width);
      points[i].y = random(height);
      points[i].speedX = random(-5, 5);
      points[i].speedY = random(-5, 5);
      points[i].speedX = base_speed*points[i].speedX/sqrt(sq(points[i].speedX)+sq(points[i].speedY));
      points[i].speedY = base_speed*points[i].speedY/sqrt(sq(points[i].speedX)+sq(points[i].speedY));
      points[i].ballsize = default_ballsize;
      points[i].col1 = random(0, 360);
      points[i].col2 = random(90, 100);
      points[i].col3 = random(90, 100);
    }
    // 演出のため、ボールの位置の初期化を50回繰り返した後でreset_flagをfasleに戻す
    if (counter >= 50){
      counter = 0;
      reset_flag = false;
    }
  }
  
  // 動画作成用にpngファイルを保存　※保存時にコメントインする
  //saveFrame("frames1/######.png");
}

class Point {
  // 変数を宣言
  float x;  //
  float y;
  float speedX;
  float speedY;
  float ballsize;
  float col1; 
  float col2;
  float col3;

  // constractorを初期化
  Point(float _x, float _y, float _speedX, float _speedY, float _ballsize,
        float _col1, float _col2, float _col3) {
    x = _x;
    y = _y;
    speedX = _speedX;
    speedY = _speedY;
    ballsize = _ballsize;
    col1 = _col1;
    col2 = _col2;
    col3 = _col3;
  }

  // method 関数
  void move() {
    // x,y方向にそれぞれ移動
    x += speedX;
    y += speedY;
    
    // 玉が左端に到達したらx軸方向を逆向きにする
    // ※半径の幅を考慮してballsize/2としている
    if (x < ballsize/2){
      x = ballsize/2;
      speedX = -speedX;
    }
    // 玉が右端に到達したらx軸方向を逆向きにする
    else if (x > width-ballsize/2) {
      x = width-ballsize/2;
      speedX = -speedX;
    }
    // 玉が上端に到達したらy軸方向を逆向きにする
    if (y < ballsize/2){
      y = ballsize/2;
      speedY = -speedY;
    }
    // 玉が下端に到達したらy軸方向を逆向きにする
    else if (y > height-ballsize/2){
      y = height-ballsize/2;
      speedY = -speedY;
    }
  }
  
  // 描画 
  void drawEllipse() {
    // 縁なし
    noStroke();
    
    // 玉の色を指定
    fill(col1, col2, col3, 90);
    
    // 位置とサイズを指定して、玉を表示
    ellipse(x, y, ballsize, ballsize);
  }
}

だいぶやりたいことが表現できるようになってきました。今回で、一旦、Processingの実践は終わりにしますが、また作りたいアニメーションができたら紹介します。
最後まで読んでいただきありがとうございました。

2022-08-16

二項分布が正規分布に近似する様子をアニメーションにしてみた｜Processing

Processing

今回も前回に続き、Processingを使ってアニメーションを作成しました。今回は、Processingについて更に理解を深めるために、クラスを使ってみました。

アニメーションイメージ

ボールが50％の確率で左か右に振れながら落ちていく時、最終的な落下位置は二項分布に従うとみなせます。

また、試行回数が大きいとき、二項分布は、正規分布に近似できることが知られています。
今回、500個のボールを落とした時の様子をProcessingで実装し、その散らばりが正規分布の形になることを確認してみました。

youtube.com

アニメーションのコード

以下の点を意識して実装しました。

ボール用のクラスを作成して、位置・移動の方向・色などボールごとに異なる情報は、クラスのフィールドに持たせる
ボールに関する処理（移動、描画）をクラスのメソッドとして定義する
それ以外の要素は、グローバル変数として管理する

以下がコードになります。

// 二項分布が正規分布に近似する様子

// 変数宣言
int t = 0;  // 時間管理用変数
int ballnum = 500;  // 玉の数（初期値）
int ballsize = 11;  // 玉のサイズ（初期値）
float surface_rate = 0.65;  // 水面の位置
boolean reset_flag = false;  // リセットフラグ
int reset_count = 0;  // リセットタイミング調整用のカウンタ
Ball[] balls = new Ball[ballnum];  // 玉の配列

// 初期化　最初に1回だけ実行される
void setup() {
  // フレームレート(1秒ごとに表示されるフレーム数)を指定
  frameRate(10);
  
  // 画面サイズを指定
  //fullScreen(); // フルスクリーン用
  size(540, 980); // 縦長表示用
  
  // カラーモード指定
  colorMode( HSB, 360, 100, 100, 100 );
  
  // 初期化
  for (int i=0; i<balls.length; i++) {
    balls[i] = new Ball(width/2  // x座標
                          ,ballsize*3  // y座標
                          ,ballsize  // x軸方向への移動幅
                          ,ballsize+2  // y軸方向への移動幅
                          ,random(0, 360)  // 色相
                          ,random(50, 60)  // 彩度
                          ,random(90, 100));  // 明度
  }
}

// 図形を描画　ループして実行されるためアニメーションになる
void draw() {
  // 背景色
  background(0,0,100);
  
  // 水色の四角を描画
  noStroke();
  fill(180,100,100,10);
  rect(0, height*surface_rate, width, height);

  // 玉の描画と移動
  for (int i=0; i<balls.length; i++) {
    // 時間tの値に応じて、配列内の玉を1つずつ動かし始める
    if (t > i){
      balls[i].drawEllipse();
      balls[i].move();
    }
  }

  // 玉同士の接触判定
  for (int i=0; i<balls.length; i++) {
    for (int j=i+1; j<balls.length; j++) {
      
      // 落下の開始地点付近では判定はしない
      if ((balls[i].y <= ballsize*4) || (balls[j].y <= ballsize*4)) {continue;}
      
      // 玉の中心同士の距離 = √((x1-x2)^2+(y1-y2)^2)
      float dist = sqrt(sq(balls[i].x - balls[j].x) + sq(balls[i].y - balls[j].y));
      
      // 玉のサイズより近づいたら接触とみなして動きを止める
      if (dist < ballsize) {
        balls[j].speedX = 0;
        balls[j].speedY = 0;
        // 0.4個分ずらして積み上げる
        balls[j].y=balls[i].y - ballsize*0.4;
        continue;
      }
    }
  }

  // リセット判定
  int sum_speedY = 0;
  // 全ての玉の落下速度(sppedY)の和を計算
  for (int i=0; i<balls.length; i++) {
    sum_speedY += balls[i].speedY;
  }
  // 0になっていたらreset_flagをtrueにする
  if (sum_speedY == 0){
    reset_flag = true;
    reset_count++;
  }  
  
  // リセット処理  ※30フレーム分制止する
  if (reset_flag && reset_count > 30){
    
    // ボールの位置などを全て初期化
    for (int i=0; i<ballnum; i++) {
      balls[i].x = width/2;  // x座標
      balls[i].y = ballsize*3;  // y座標
      balls[i].speedX = ballsize;  // x軸方向への移動幅
      balls[i].speedY = ballsize+2;  // y軸方向への移動幅
      balls[i].col1 = random(0, 360);  // 色相
      balls[i].col2 = random(50, 60);  // 彩度
      balls[i].col3 = random(90, 100);  // 明度
    }
    reset_flag = false;
    reset_count = 0;
    t = 0;
  }
  
  // 動画作成用にpngファイルを保存　※保存時にコメントインする
  //saveFrame("frames/######.png");
  
  // 時間を進める
  t+=1;
}

// クラスを定義
class Ball {
  // フィールド変数を宣言
  float x;  // x座標
  float y;  // y座標
  float speedX;  // x軸方向への移動幅
  float speedY;  // y軸方向への移動幅
  float col1;  // 色相
  float col2;  // 彩度
  float col3;  // 明度

  // constractorを初期化
  Ball(float _x, float _y, float _speedX, float _speedY,
        float _col1, float _col2, float _col3) {
    x = _x;
    y = _y;
    speedX = _speedX;
    speedY = _speedY;
    col1 = _col1;
    col2 = _col2;
    col3 = _col3;
  }

  // メソッド関数
  // 玉を移動
  void move() {
    // y軸方向に移動
    y += speedY;
    
    // x軸方向への移動は、水面より上では、ランダムで左右に動く
    if (y < height*surface_rate){
      if ((int)random(2)%2 == 0){
        x += speedX;
      }else{
        x -= speedX;      
      }
    }
    
    // 下端に到達したらy方向への移動を止める
    if (y > height-ballsize){
      speedY = 0;
      y = height-ballsize/2;
    }
  }
  
  // 玉を描画 
  void drawEllipse() {
    // 縁なし
    noStroke();
    
    // 玉の色を指定
    fill(col1, col2, col3, 100);
    
    // 位置とサイズを指定して、玉を表示
    ellipse(x, y, ballsize, ballsize);
  }
}

まとめ

クラスを使うことで、コードが構造化できた気がします。
今回は、200行弱のコードとなりましたが、コードの読みやすさと備忘のために改行やコメントを多めに入れている分を踏まえると、実際は100行程度で書けると思います。また私自身がProcessing初心者のため、冗長な部分もあると思います。もし、バグなどにお気づきの方は、ご指摘いただけると嬉しいです。
もう少しProcessingを使って色々描いてみて、スキルアップしたいと思います。

最後まで読んでいただきありがとうございました！

2022-07-25

Processingで元気玉風のデジタル動画を作成

Processing

今回は、Processingというプログラミング言語を初めて使用してみました。Processingは、Javaを単純化してグラフィック機能に特化した言語と言われています。複雑なセットアップ作業も不要であるため、プログラミング初心者でも比較的に簡単に始められます。

作成した動画

元気玉風の球体が徐々に大きくなっていくイメージの動画を作成しました。
youtu.be

Processingの準備

実行ファイルのダウンロード

「processing programming」と検索し、公式サイトへアクセスします。

ダウンロードページから、自身の環境に合った実行ファイルをダウンロードします。※2022.07時点でversion 4.0はまだベータ版（試用版）なので、私は正式版の3.54を取得しました。

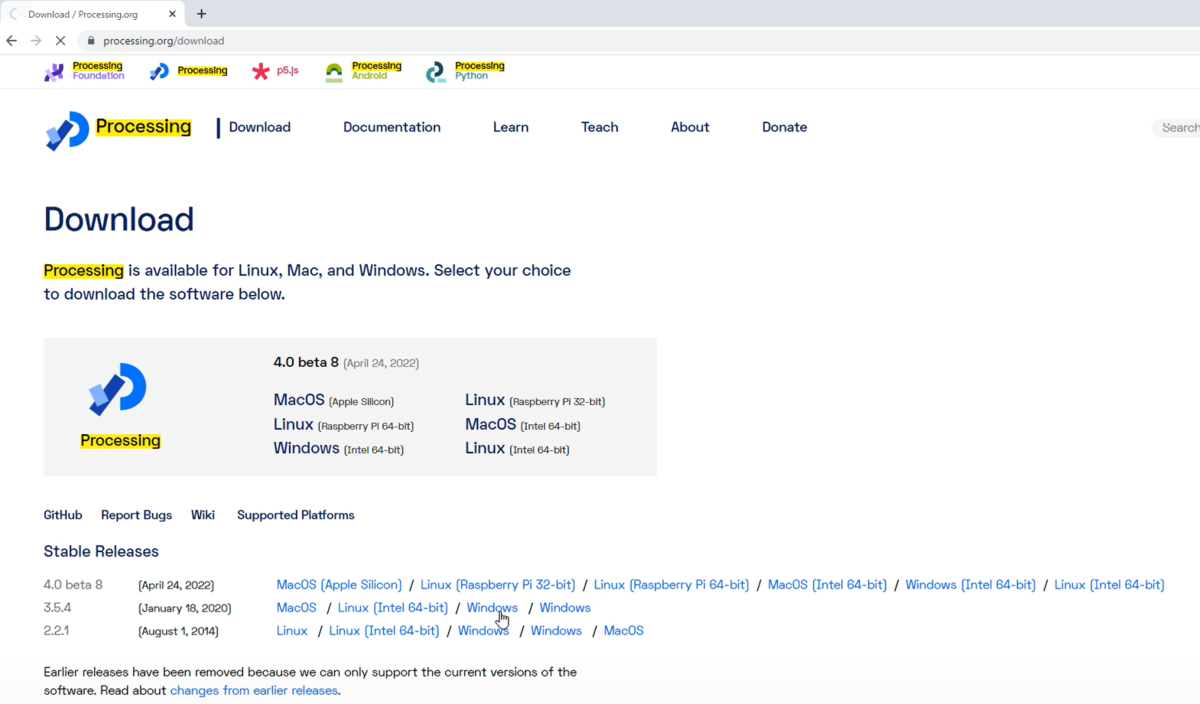
Processingの起動

Windows版の実行ファイルはzipファイルになっていますので、適当なフォルダーに展開します。※例：「C:\Program Files\processing-3.5.4-windows64\processing-3.5.4」

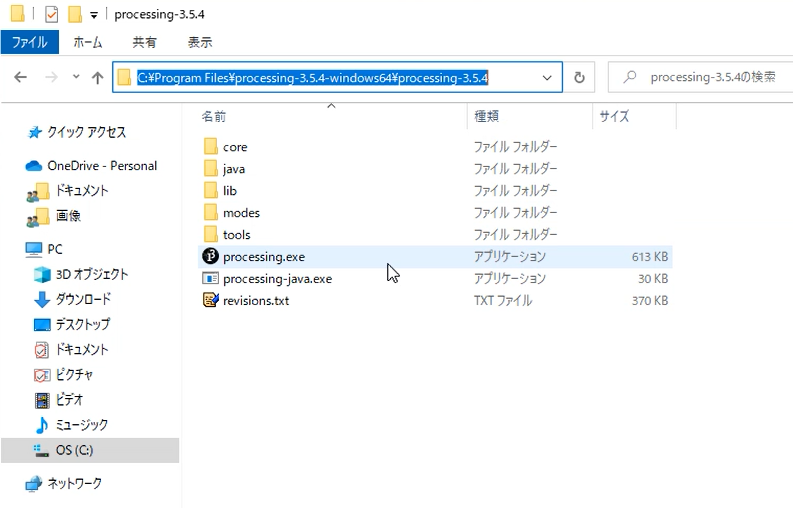
processing.exeが実行ファイルなので、これをクリックして起動します。processing.exeのショートカットをデスクトップ等に作成すると便利です。

エディタが表示されます。Processingの起動が出来ました。

エディタのフォント設定

「ファイル」→「設定」をクリックします。

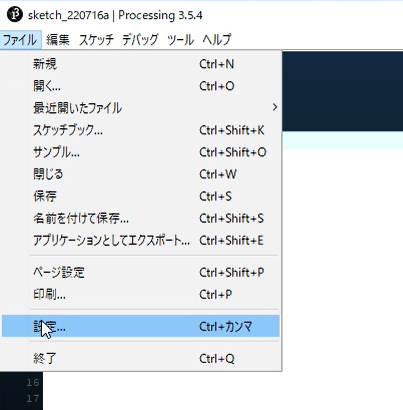
日本語対応フォントへの変更

「エディタとコンソールのフォント」から、「MSゴシック」など日本語入力が可能なフォントに変更します。

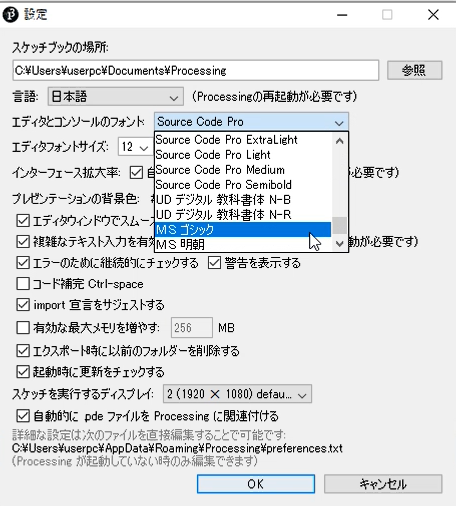
フォントサイズ

エディタのフォントサイズはデフォルトだと「12」で小さいため、「18」くらいに変更することをお勧めします。

これで、Processingを使う準備が出来ました。他のプログラミング言語と比べて、とても簡単です。

サンプルコードの実行

エディタ部分にコードを書いて、実行ボタンを押します。

別ウィンドウが起動され、プログラムの実行結果が表示されます。

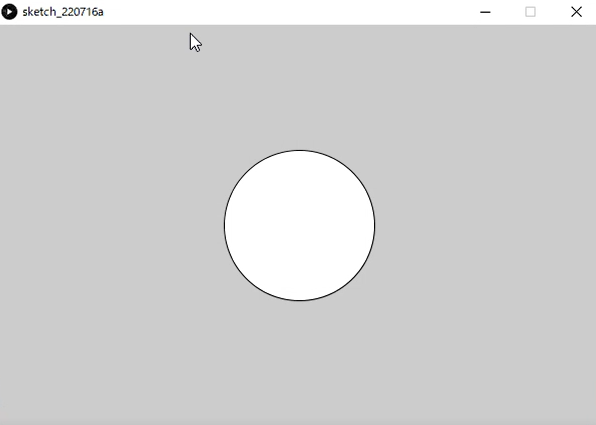
元気玉風アニメーションのコード

では、元気玉風のアニメーションを作成してみましょう。以下のコードをコピー＆ペーストして実行すれば、冒頭で紹介したアニメーションが起動されると思います。

// 元気が溜まる動画

// 変数宣言
int t = 1;  // 時間管理
int cnt = 0;  //ループカウンタ
int org_ball_num = 60;  // 小エネルギー玉の個数（初期値）
int cur_ball_num = org_ball_num;  // 小エネルギー玉の個数（最新値）
int param1 = 50;  // 大エネルギー玉の外側オーラの幅
int param2 = 700;  // 小エネルギー玉の生成が止まるタイミング
int param3 = 750;  // 各パラーメータのリセットタイミング
float power_size = 5;  // 小エネルギー玉のサイズ
float range = 10;  // 小エネルギー玉が消える範囲
float[] x = new float[cur_ball_num];  // 小エネルギー玉のx座標のリスト
float[] y = new float[cur_ball_num];  // 小エネルギー玉のy座標のリスト
float[] dist_x = new float[cur_ball_num];  // 画面中心からのx方向の距離
float[] dist_y = new float[cur_ball_num];  // 画面中心からのy方向の距離
// 画面タイプを指定　Default:正方形、SP:縦長、PC:横長
String mode = "PC"; // "Default" or "SP" or "PC"

// 初期化　最初に1回だけ実行される
void setup(){
  // フレームレート(1秒ごとに表示されるフレーム数)を指定
  frameRate(30);
  
  // 画面サイズを指定
  // ※size関数には変数は使えないため、画面タイプに合わせて手動修正
  //size(1000, 1000, P3D); // Default
  //size(540, 980, P3D); // SP
  size(1920, 1080, P3D); // PC

  // 小エネルギー玉の位置を初期化
  for(int i = 0; i < cur_ball_num; i++){
    x[i] = random(width);
    y[i] = random(height);
  }

  // 画像タイプごとにパラメータを調整
  if (mode == "SP"){
    param1 = 40;
    param2 = 680;
    param3 = 740;
  }
  else if (mode == "PC"){
    param1 = 50;
    param2 = 750;
    param3 = 800;
  }
  
  // tを各パラーメータのリセットタイミングの直前に設定
  t = param3 - 1;
}

// 図形を描画　ループして実行されるためアニメーションになる
void draw(){
  
  // 小エネルギー玉を描画
  for(int i = 0; i < cur_ball_num; i++){
    if (cnt == 0) {break;}
    // 枠線なし
    noStroke();
    
    // 色を指定
    fill(190, 248, 253, 255);
    
    // 位置とサイズを指定
    ellipse(x[i], y[i], power_size, power_size);
    
    // 画面の中心からの距離を取得(x軸、y軸)
    dist_x[i] = max(x[i] - width/2, width/2 - x[i]);
    dist_y[i] = max(y[i] - height/2, height/2 - y[i]);

    // 中央付近に入ったら、位置を初期化する
    if (dist_x[i] + dist_y[i] <= range*5){
      x[i] = random(width);
      y[i] = random(height);
    }

    // x軸方向の移動
    if (x[i] > width/2 + range){
      // 真ん中+rangeよりも右側にいる場合は、x座標の値を減らす（左に移動）
      x[i] -= (x[i] - width/2 + range)/50;
    }
    else if (x[i] < width/2 - range){
      // 真ん中-rangeよりも左側にいる場合は、x座標の値を増やす（右に移動）
      x[i] += (width/2 - range - x[i])/50;
    }
    else {
      // それ以外(真ん中付近)にいる場合は、真ん中に移動
      x[i] = width/2;
    }
    
    // y軸方向の移動
    if (y[i] > height/2+range){
      // 真ん中+rangeよりも下側にいる場合は、y座標の値を減らす（上に移動）
      y[i] -= (y[i]-height/2+range)/50;
    }
    else if (y[i] < height/2-range){
      // 真ん中-rangeよりも上側にいる場合は、y座標の値を増やす（下に移動）
      y[i] += (height/2-range-y[i])/50;
    }
    else {
      // それ以外(真ん中付近)にいる場合は、真ん中に移動
      y[i]=height/2;
    }
  }
  
  // 時間の経過とともに、小エネルギー玉の表示を変えていく
  power_size += 0.04;  // サイズを大きくする
  range += 0.015;  // リセットするレンジを広くする
  cur_ball_num = org_ball_num - floor(org_ball_num * t/param2);  //表示数を減らす
  
  // 以下、大エネルギー玉を描画
  
  // 原点を中心に移動
  translate(width/2, height/2, 50);
  
  // 1層目 外側のエネルギー
  // 色埋めしない
  noFill();
  // 枠を表示　色を時間経過とともに、変化させていく
  stroke((t + 600)/2 - 450,(t + 600)/2,((t + 600)/2)*9,20);
  // 半径t+param1の球体を表示
  sphere(t + param1);
  
  // 2層目 内側のエネルギー
  // エネルギーの色を指定
  fill(141,242,253,100);
  // 半径tの球体を表示
  noStroke();
  sphere(t);

  // 3層目　この動画の背景色になる
  fill(0, 0, 0);  // 黒で埋める
  // 2層目よりも一回り小さい半径(t-10)の球体を表示する
  if (t > param2){
    noStroke();
    sphere(t - 10);
  }
    
  // 一定時間を超えたら、パラメータをリセットする
  if (t > param3){
    t = 0;
    range = 10;
    power_size = 5;
    cur_ball_num = org_ball_num;
    cnt+=1;
  }
  
  // 動画作成用にpngファイルを保存　※保存時にコメントインする
  //saveFrame("frames/######.png");

  // tをインクリメント
  t+=1;
}

動画ファイルの保存

プログラムの中でsaveFrame関数を実行すると、プログラムを停止するまでの間、コマ送りで画像ファイルが生成されていきます。

saveFrame("frames/######.png");

画像ファイルが出来たら、「ツール」→「ムービーメーカー」から、画像ファイルの格納フォルダを指定し、「動画を作成」をクリックします。

作成された動画は「.mov」という拡張子のファイルで、基本的にWindowsでは再生できない形式となります。
MOVで保存した後で、mp4などWindowsで再生可能な形式に変換します。（変換ソフトウェアはたくさん公開されており、難しくありませんのでここでは割愛します。）

これで、アニメーション動画の完成です。

まとめ

Processingを使ってアニメーション動画を作成する方法を紹介しました。
Processingは、実行ファイルを起動するだけで使用でき（インストール・セットアップ作業が不要）、また、図形を描画するための関数が用意されており、短い行数でプログラムが書けます。そのため、プログラミング初心者でも簡単に始められると感じました。
また、Processingのダウンロードからサンプルコードの実行まで、実際に操作している様子を動画にまとめました。もし記事の中で不明点があれば、こちらもご確認ください。
youtu.be

本記事が皆様のお役に立てば幸いです。
最後まで読んでいただきありがとうございました！

2022-05-22

Googleデータポータル使い方

データ可視化

今回は、Googleデータポータルの使い方を紹介します。最近、私の職場で使用しているデータベースシステムが、オンプレミスからクラウドのGoogle BigQueryに移行したのを受けて、BIツールについても今後、Googleデータポータルが職場におけるメインの選択肢になると思い、勉強し始めました。まずは、見よう見まねで使ってみた時のフローを、備忘を兼ねて整理しました。

データポータルの初回設定

データポータルのURLにアクセスします。
https://datastudio.google.com

左上の「作成」→「レポート」をクリックします。

国名を選択し、利用規約にチェックを入れて、「続行」をクリックします。会社名は空欄のままでも大丈夫です。

メールの設定はお好みで選択して、「続行」をクリックします。

データの追加

データポータルでは、様々なデータ形式をサポートしていますが、今回は、Google スプレッドシートのデータを使用します。
以下のサイトで公開されているサンプルデータを使用します。
http://l.rw.rw/trydatastudio

コピーを作成します。自身のアカウントのGoogle driveに保存されます。

改めて、データポータルに戻り、再度、「作成」→「レポート」をクリックします。

Google スプレッドシートを選択します。

先ほどアクセスしサンプルデータを選択し、「追加」をクリックします。

テーブルデータの編集

デフォルトで適当な項目が選択されている状態のテーブルデータが表示されます。

右側のディメンジョンから、表の項目を追加・変更することが出来ます。

編集後のイメージはこちらです。

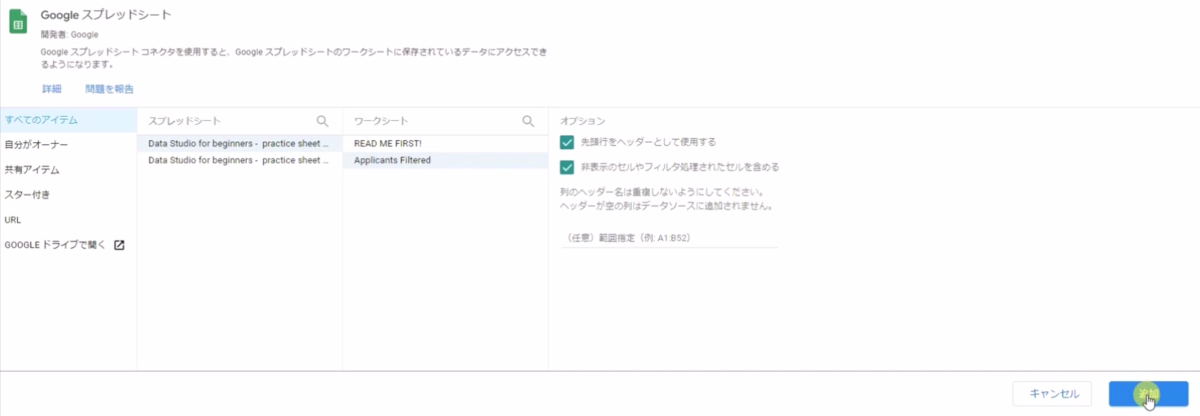
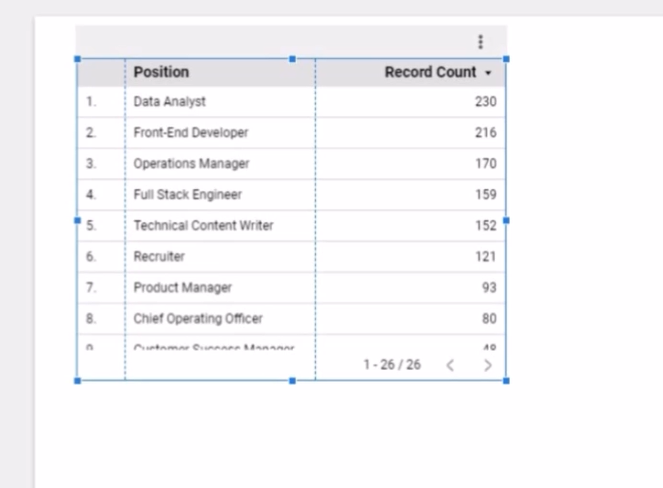
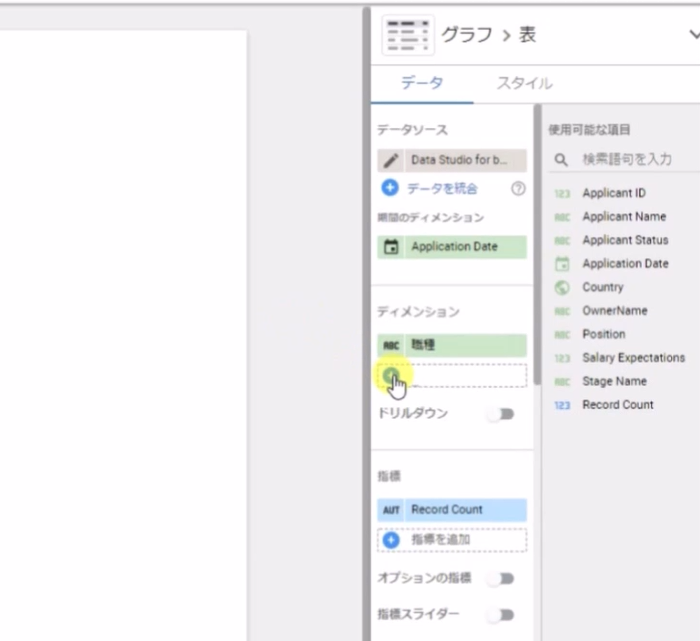
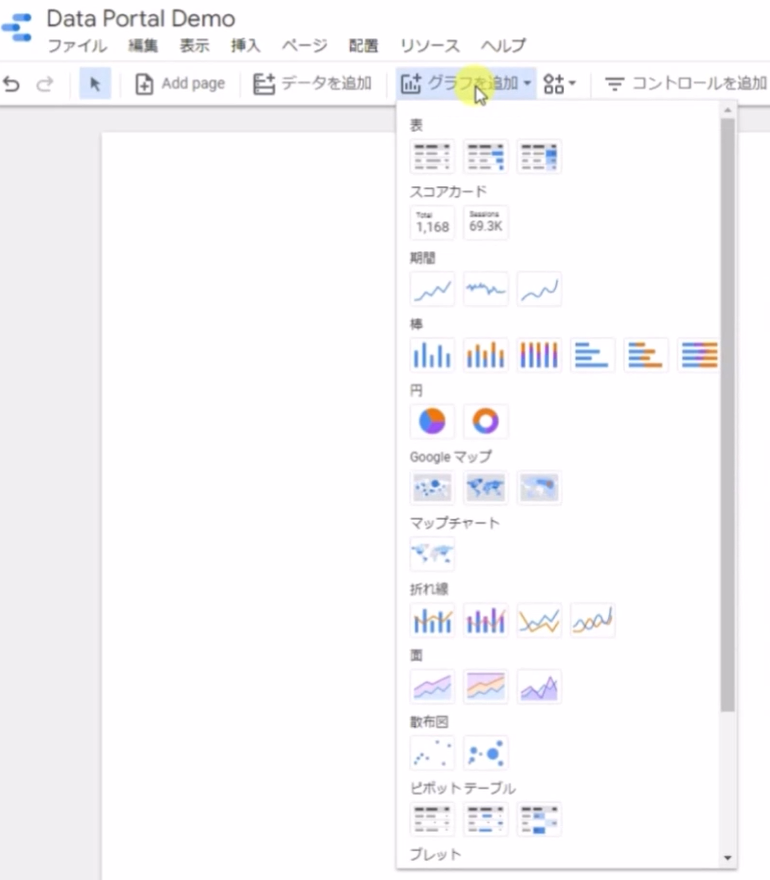
その他のグラフを追加

メニューから「グラフを追加」を選択すると、様々なグラフを追加することができます。

イメージ：

まとめ

Googleデータポータルの使い方について簡単ではありますが紹介させていただきました。本記事が少しでもお役に立てば幸いです。
今回も、実際にPCで操作している様子を動画にまとめました。よければこちらもご確認ください。
youtu.be

最後まで読んでいただき、ありがとうございました。

2022-03-20

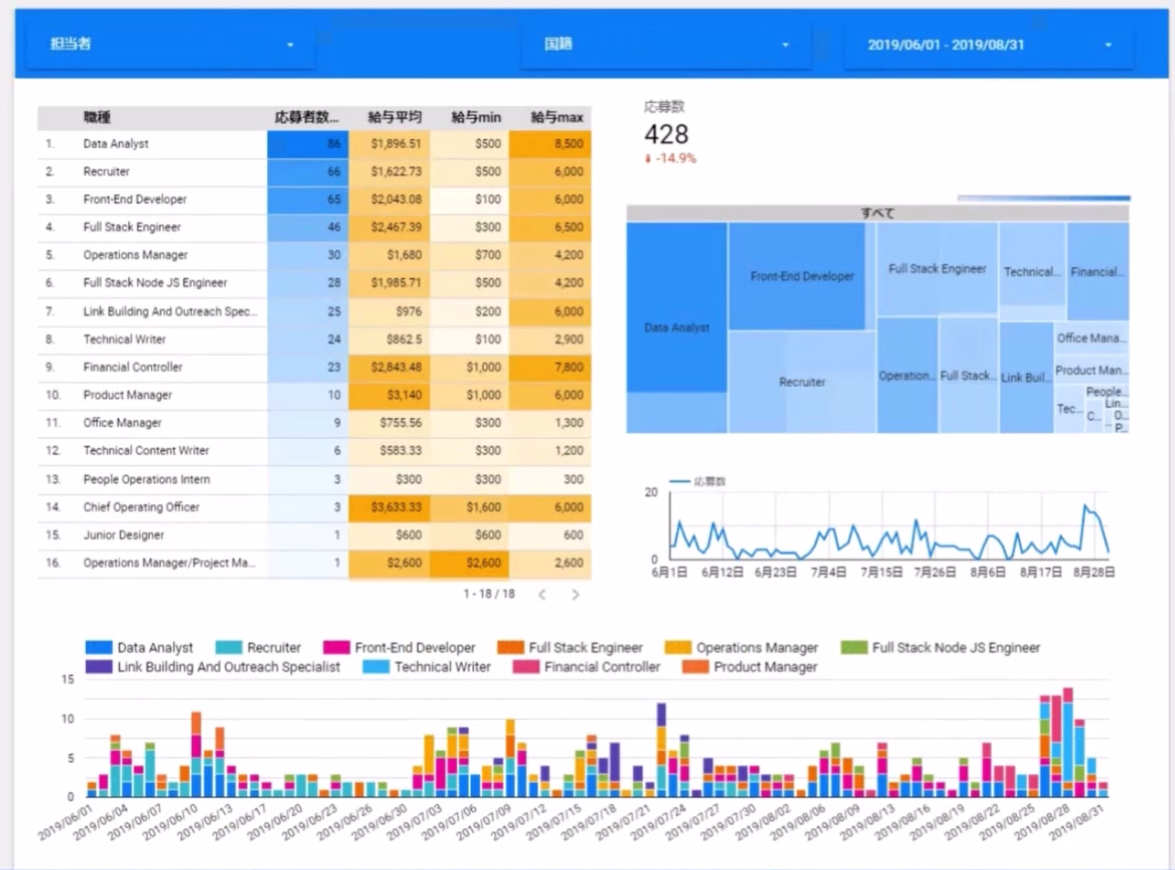
確率分布の期待値・分散・母関数まとめ～連続分布～

統計検定対策

以前の記事に続き、統計検定1級/準1級の対策として、各確率分布の期待値・分散・母関数について整理しました。
今回は、連続分布を扱いました。
離散分布のまとめについてはこちらを参照ください。
確率分布の期待値・分散・母関数まとめ～離散分布～ - Kevin's Data Analytics Blog

1. 連続一様分布

定義

𝑎<𝑥<𝑏の連続値をとる確率変数𝑋に対して、確率密度関数の値が常に一定であるような確率分布を連続一様分布という。

確率密度関数

$f(x)=\dfrac{1}{b-a}$

期待値

$E(X)=\dfrac{a+b}{2}$

分散

$V(X)=\dfrac{(b-a)^{2}}{12}$

積率母関数（モーメント母関数）

$E(t^{tX})=\dfrac{e^{tb}-e^{ta}}{t(b-a)}$

2. 正規分布

定義

𝜇∈"ℝ, " σ>0とし、確率変数𝑋に対して、以下の確率密度関数をもつ分布を正規分布という。𝜇を中心する左右対称の釣鐘型の分布になっている。

確率密度関数

$f(x)=\dfrac{1}{\sqrt{2\pi\sigma}}\exp(-\dfrac{(x-\mu)^ 2}{2\sigma^ 2})$

期待値

$E(X)=\mu$

分散

$V(X)=\sigma^ 2$

積率母関数（モーメント母関数）

$E(t^{tX})=\exp(\mu t+\dfrac{\sigma^2 t^2}{2})$

3. 指数分布

定義

　λ>0とし、確率変数𝑋に対して、以下の確率密度関数をもつ分布を指数分布という。単位時間あたり平均λ回起こる現象の発生間隔の確率分布を表している。

確率密度関数

$f(x)=\lambda e^{-\lambda x}$

期待値

$E(X)=\dfrac{1}{\lambda}$

分散

$V(X)=\dfrac{1}{\lambda ^2}$

積率母関数（モーメント母関数）

$E(t^{tX})=\dfrac{\lambda}{\lambda - t} \quad (t < \lambda)$

4. ガンマ分布

定義

　α>0, 𝛽>0 とし、確率変数𝑋に対して、以下の確率密度関数をもつ分布をガンマ分布という。ガンマ分布は単位時間あたり平均𝛽回起こる現象がα回起こるまでの時間の確率分布を表している。

確率密度関数

$f(x)=\frac{\beta^{\alpha}}{\Gamma(\alpha)}x^{\alpha-1}e^{-\beta x} \quad (x>0)$

※ガンマ関数の定義は以下のとおり

$\Gamma(x)=\displaystyle\int_{0}^{\infty}t^{x-1}e^{-t}\,dt$

期待値

$E(X)=\dfrac{\alpha}{\beta}$

分散

$V(X)=\dfrac{\alpha}{\beta ^2}$

積率母関数（モーメント母関数）

$E(t^{tX})=(\dfrac{\beta}{\beta - t})^{\alpha}$

5. ベータ分布

定義

　α>0, 𝛽>0 とし、確率変数𝑋に対して、以下の確率密度関数をもつ分布をベータ分布という。

確率密度関数

$f(x)=\dfrac{1}{B(\alpha , \beta)}x^{\alpha -1}(1-x)^{\beta -1}$

※ベータ関数の定義は以下のとおり

$B(\alpha , \beta)=\displaystyle\int_{0}^{1}x^{\alpha-1}(1-x)^{\beta -1}\,dt$

期待値

$E(X)=\dfrac{\alpha}{\alpha + \beta}$

分散

$V(X)=\dfrac{\alpha\beta}{(\alpha + \beta)^2(\alpha + \beta +1)}$

積率母関数（モーメント母関数）

　簡単な式で表せない

6. コーシー分布

定義

　確率変数𝑋に対して、以下の確率密度関数をもつ分布をコーシー分布という。

確率密度関数

$f(x)=\dfrac{1}{\pi} \dfrac{1}{x^2 +1}$

期待値

　存在しない

分散

　存在しない

積率母関数（モーメント母関数）

　存在しない

7. 対数正規分布

定義

𝑌~N(𝜇, 𝜎^2) のとき、確率変数𝑋= $𝑒^𝑌$ が従う確率分布を対数正規分布という。確率密度関数は以下のとおり。

確率密度関数

$f(x)=\dfrac{1}{\sqrt{2\pi\sigma}}\dfrac{1}{x}\exp(-\dfrac{(\log x-\mu)^ 2}{2\sigma^ 2})$

期待値

$E(X)=\exp(\mu +\dfrac{\sigma ^2}{2})$

分散

$V(X)=\exp(2\mu +\sigma ^2)(\exp(\sigma ^2) -1)$

積率母関数（モーメント母関数）

　存在しない

8. ワイブル分布

定義

　𝑎>0, 𝑏>0 とし、確率変数𝑋に対して、以下の確率密度関数をもつ分布をワイブル布という。

確率密度関数

$f(x)=\dfrac{b}{a^b}x^{b-1}\exp(-(\dfrac{x}{a})^b)$

なお、ワイブル分布は、ガンマ関数における定数λを、以下の式で 𝑥の関数とした場合の分布である。

$\lambda=\gamma(x)=cx^{b-1}, \quad c=\dfrac{b}{a^b}$

𝑏=1 のときのワイブル分布は、𝑟(𝑥)=𝑐で一定となり、指数分布になる。

期待値

$E(X)=\alpha\Gamma(\dfrac{b+1}{b})$

分散

$V(X)=\alpha^2(\Gamma(\dfrac{b+2}{b}) - \Gamma(\dfrac{b+1}{b})^2)$

積率母関数（モーメント母関数）

　簡単な式で表せない

9. ロジスティック分布

定義

　確率変数𝑋に対して、以下の確率密度関数をもつ分布をロジスティック分布という。

確率密度関数

$f(x)=\dfrac{e^{-x}}{(1+e^{-x})^2}$

また、ロジスティック分布の累積分布関数は、ロジスティック関数である。

$P(X\le x)=\dfrac{1}{1+e^{-x}}$

期待値

$E(X)=0$

分散

$V(X)=\dfrac{\pi^2}{3}$

積率母関数（モーメント母関数）

$E(t^{tX})=\Gamma(1+t)\Gamma(1-t)$

導出方法

多くの参考書において、これらの導出は、数式の途中計算や公式等の前提知識の説明が省略されていることが多いため、理解に時間がかかると感じていました。
前回同様、今回も自分用に整理したものを、動画にしてみました。途中の流れを細かく説明しています。必要に応じてご確認ください。
youtu.be

対策本

統計検定1級/準1級の対策本としては、以下の書籍があります。

日本統計学会公式認定統計検定1級対応統計学

作者:二宮嘉行,大西俊郎,小林景,椎名洋,笛田薫,田中研太郎,岡田謙介,大屋幸輔,廣瀬英雄,折笠秀樹
東京図書

Amazon

こちらの書籍は、検定の範囲内のトピックが幅広く網羅されていますが、数式や解説が省略されている個所が多い印象です。あくまでも、出題範囲のトピックを確認するための用途として使用し、詳細の内容はインターネット等で確認し理解を深めるのが良いと思います。

まとめ

確率分布の期待値・分散・母関数について整理しました。また、導出方法についてまとめた動画および、対策本について紹介しました。
本記事が、統計検定の対策を進める上で、お役に立てば幸いです。

2022-03-06

PythonでSQLiteのデータを読み込む方法

SQL

今回は、PythonからSQLiteのデータベースにアクセスしてSQLの実行してデータを読み込む方法を紹介します。
Pythonでデータを読み込んで処理するメリットは次の点が挙げられます。

PythonのPandasライブラリでは、データを効率的に処理するための便利な機能が多く提供されている
Pythonには機械学習を適用するためのライブラリも用意されている
その他、プログラミング言語として、SQLよりもできることが多い

ライブラリのインポート

PythonでSQLiteデータを読み込むため、Pandasとsqlite3を使用します。どちらのライブラリも標準ライブラリのため追加インストールは不要です。

import pandas as pd
import sqlite3

SQLiteに接続

sqlite3.connect関数を使用して、SQLiteのデータファイルに接続します。関数の引数にデータファイルのパスを指定します。

conn = sqlite3.connect('../data/zenkoku.sqlite3')

なお、zenkoku.sqlite3は、以下のサイトから取得しました。
住所データSQL【住所.jp】

Pandasでデータの読み込み

read_sql_query関数を使用して、データベースに対してSQLを実行します。第一引数にselect文を記述し、第二引数には先ほど接続時に作成した「conn」を指定します。

data1 = pd.read_sql_query('select * from ad_address', conn)

データの中身を確認します。

data1

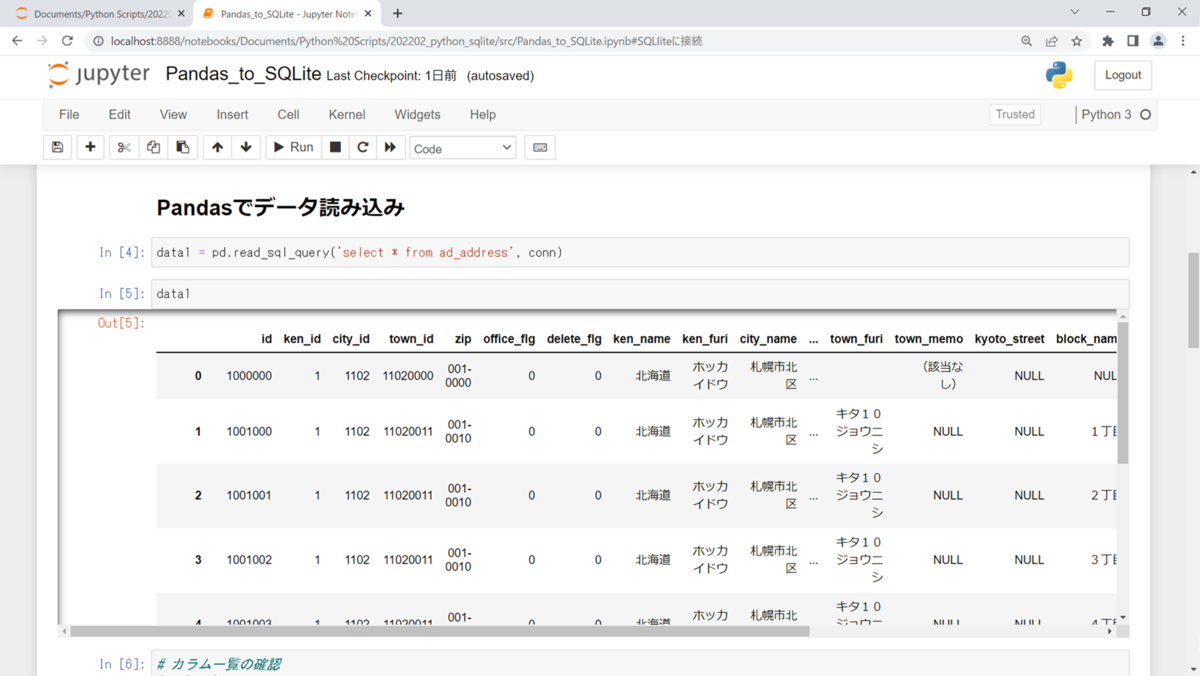
f:id:dskevin:20220220163951p:plain
データフレームの形式で読み込むことが出来ました。

改行を含む長いSQL文を記述する場合は、変数にSQL文を格納します。シングルクォーテーション3つで囲みます。

query_text='''
select
  zip
  ,ken_name
  ,city_name
  ,town_name
  ,office_name
  ,office_address
from ad_address
where ken_name = "東京都"
  and office_flg = 1
'''

同様に、read_sql_query関数を使用して、データベースに対してSQLを実行します。第一引数には、SQL文を格納した変数（query_text）を指定します。

data2 = pd.read_sql_query(query_text, conn)

データの中身を確認します。

data2

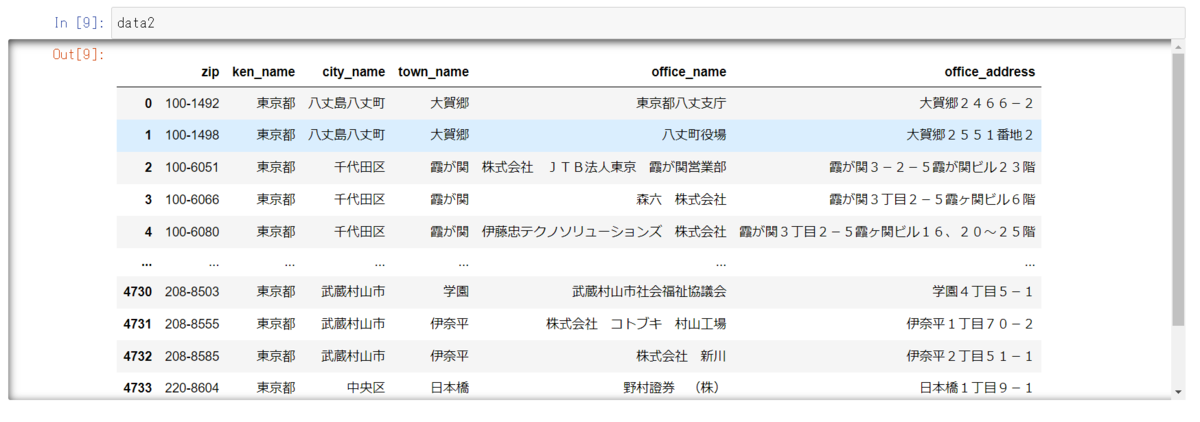
f:id:dskevin:20220220164919p:plain
クエリが実行され、クエリのwhere句に指定した条件（東京都で、office_flg=1）の住所を抽出できました。

SQLiteにデータを保存

Pandasのデータフレームを、SQLiteデータベース上の新しいテーブルとして保存することができます。
to_sql関数を使用します。第一引数には、データベース上に作成する新しいテーブル名を指定します。

data2.to_sql('office_data', conn)

以下のように、テーブルの一覧を取得して、新しくテーブルが作成されていることを確認できます。

# テーブル一覧の取得
pd.read_sql_query('select * from sqlite_master where type="table"', conn)

まとめ

Pythonを使ってSQLiteのデータを読み込む方法について紹介しました。
Python・SQLを使ってデータを扱っている方や、現在勉強中の方にとって、本記事が少しでもお役に立てば幸いです。
今回も、実際にPCで操作している様子を動画にまとめました。よければこちらもご確認ください。
youtu.be

最後まで読んでいただき、ありがとうございました！